Updated Wed. Apr. 2 Description Program 2 assignment: PDF Due date/time: Tue. Apr. 2 Official settings: nx,ny = 94; take 400 steps; dt = pi/400; cone radius 0.105, initial location (0.0, 0.3). Problem:  2-D linear advection via fractional step (directional) splitting Flow field: rotational flow (counter-clockwise), constant w/time. Methods Lax-Wendroff (from program 1), Takacs (see PDF for details), and 6th-order Crowley -- scheme available from Tremback (1987), PDF page 542, equation "ORD=6". Boundary conditions: 0-gradient in both directions (ghost point values = nearest edge value) Coding up your Program2 - notes from Class (all are PDF): From class 11: Setup, array sizes From class 12: IC and BC routines • Advection From class 13: Advection and advect1d routines From class 14: My Keeling files • Creating web pages from Pgm2 From class 15: Makefile; my Pgm2 directory • Changes from Pgm1 > Pgm2 Evaluation: Compute Takacs (1985) error statistics (eq. 6.1, 6.6, 6.7) over the entire 2-D domain after integration completed. The initial condition is the exact solution for the final time. I used sample (biased) variance, and Pearson's correlation coefficient. I provide error stats for the test case results below. Plan of attack: Get things working for Lax-Wendroff first. If you have difficulties, try running your code with everywhere (a) U=1.0 and V=0 [cone should move to right], and then (b) U=0.0 and V=-1 [cone should move downward]. Once it works for Lax-W, try Takacs, and then Crowley. Compute error stats last. FAQ/Questions+Answers section is at the bottom of this page. Notes: C programmers: be careful with array dimensions. I suggest passing NXDIM,NYDIM in your calls to subroutines, so you can define them in the routines as e.g. s1[][nydim]. With two ghost points, your s() arrays are nx+4,ny+4 points - to avoid confusion, don't hardcode the dimensions as e.g. nx+2; this is why NXDIM, NYDIM are used. Of course, you can use an include statement instead of passing parameters like NXDIM. watch your u,v indices in advection. For s1 or s2, you use array index limits i1,i2,j1,j2. For U and V, there are no ghost points, so you probably will use a separate array index or statements with e.g. [i-i1]. Contact me with questions. Contour intervals: In my plots below I used a contour interval of 0.5 -- not 1.0 -- for the scalar "s" field !! No History required: There is no need to create time-space "history" plots in program 2. So please delete the history() array declaration and the nested do- (or for-) loops used to fill in history() as we did in program 1. All: if your 1-D [ezy()] plots look blank - please DELETE any agsetf calls leftover in your code from program #1. Those were appropriate for our program 1 sine function, whose data range was about -1.2 to 1.2 ... but here our 'cone' values start out between [0,10]. Leaving the agsetf() calls out lets ezy pick the scales, which is just fine here. Test programs to show how to plot 2-D fields in Program #2 You are asked to produce contour and (optionally) surface plots for this program.  Instructions are here.  I have placed test programs to show how to call my contr and sfc, for plotting contours or surfaces, from C or Fortran, on Keeling at this location:              ~bjewett/502/Pgm2 There are also options to create movies (animated GIFs or Quicktime) in the script  metagif.  For more information, try              ~bjewett/502/Tools/metagif  -help For more information on how to use the simple contr() and sfc() routines for 2-D plotting in program 2, see this web page. There are also files in my Pgm2 directory regarding making of web pages to display your data - this will be discussed in class. Test results to evaluate your code Note the differences between the test parameters and your assignment. >> Be sure to change all these parameters back to the official problem before running & handing your results in! Settings: Note this test case used different settings from the official hand-in problem!! Domain is 51x51 Cone size (radius) was 0.120, unlike value in the hand-in problem. Time step here is pi/400 (instead of pi/600) It was run for 400 steps = 1 rotation for the pi/400 time step Dx calculated usual way (dx = 1./real(nx-1)) I plotted every 100 steps. I show both contours and surface plots below. INITIAL CONDITION plots: (scalar field contour interval = 0.5; U/V contour interval = 0.1) S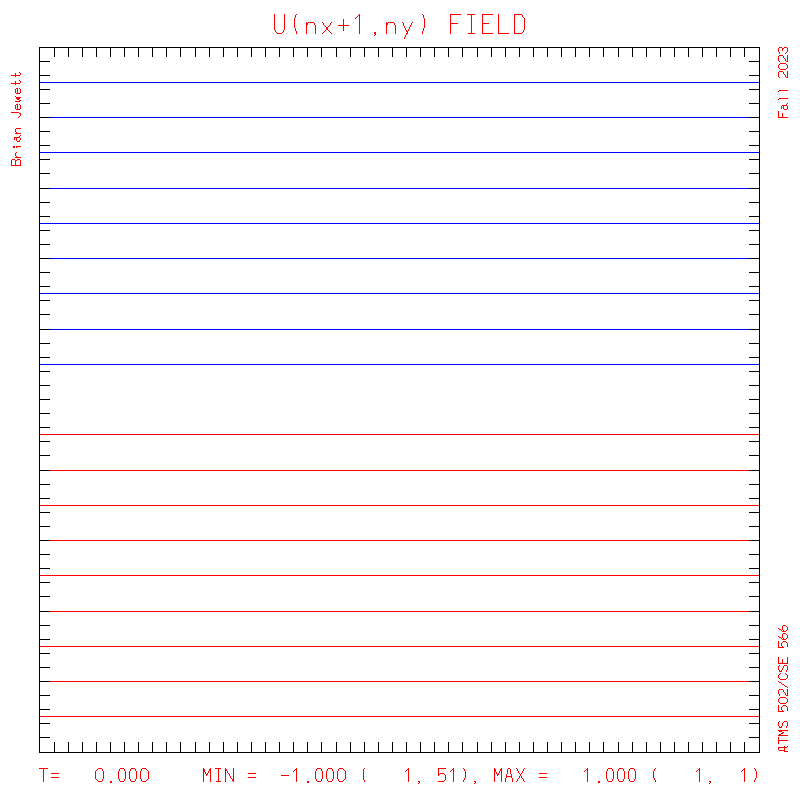 U V The text output from my program including error statistics: Lax-W, Takacs, 6th-order Crowley. To answer several questions: your error stat results need not match mine exactly, but the contour plots should be very similar to mine, and the stats should probably agree to 3 decimal places, and the dispersion + dissipation error should equal your total error. Note: my contour interval for the scalar field is 0.5 ... but the contour interval for U,V is 0.1 Test case N=100 N=200 N=300 N=400 (1 cycle) Min/max plots Lax-W contours 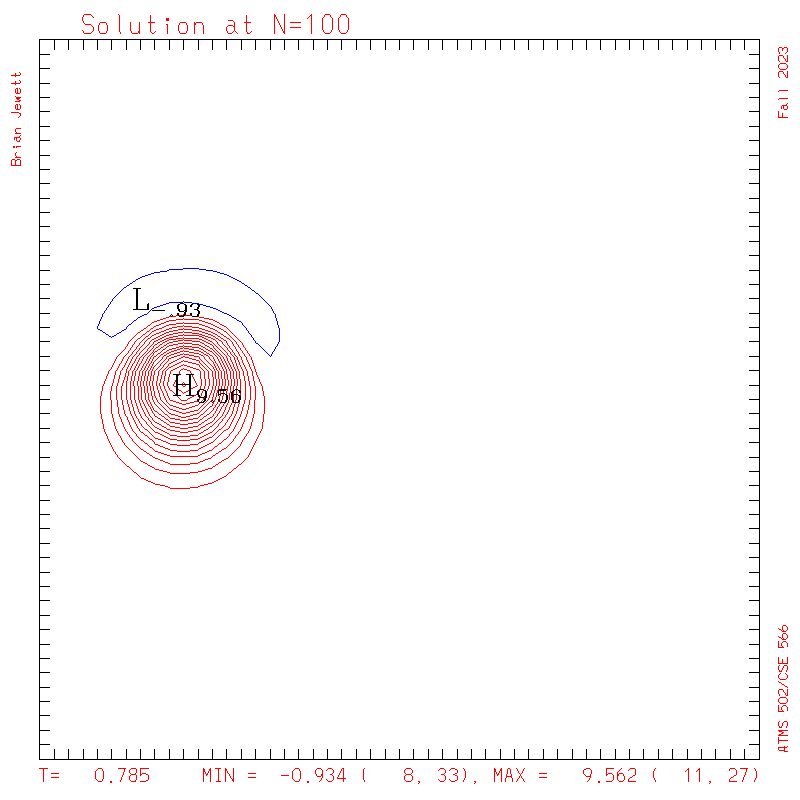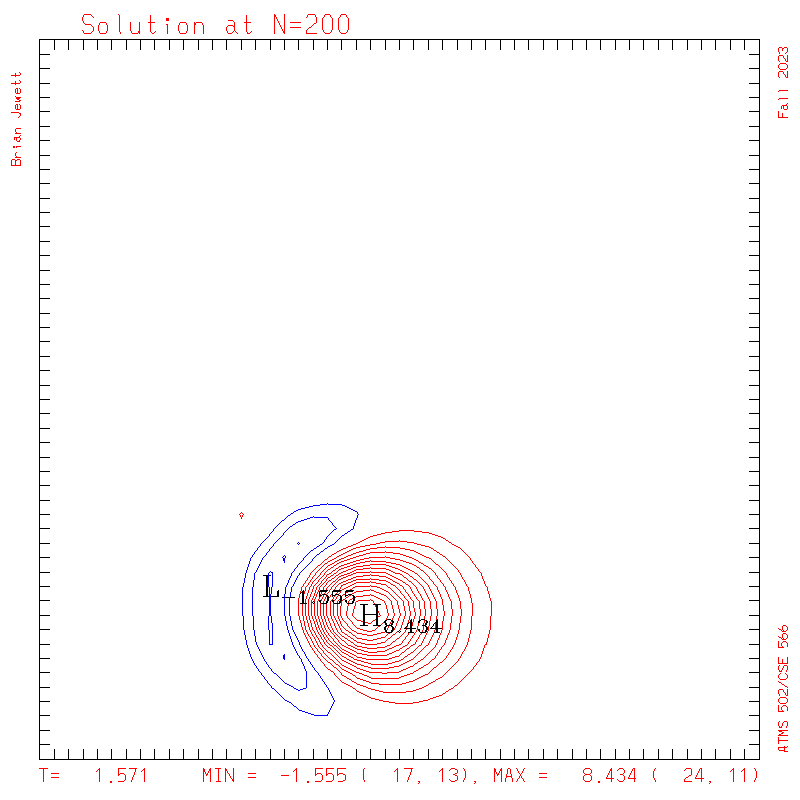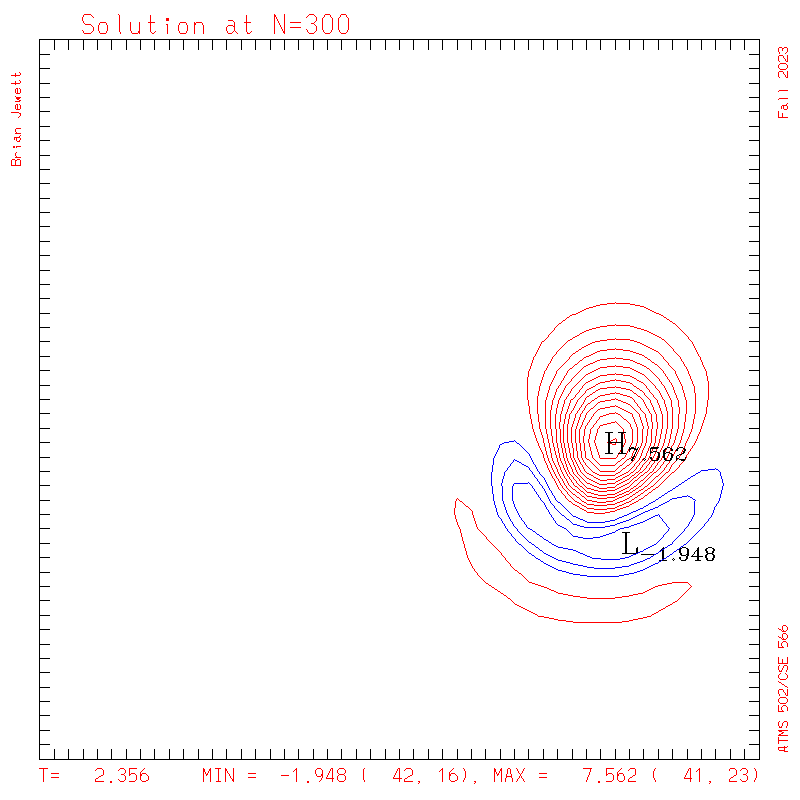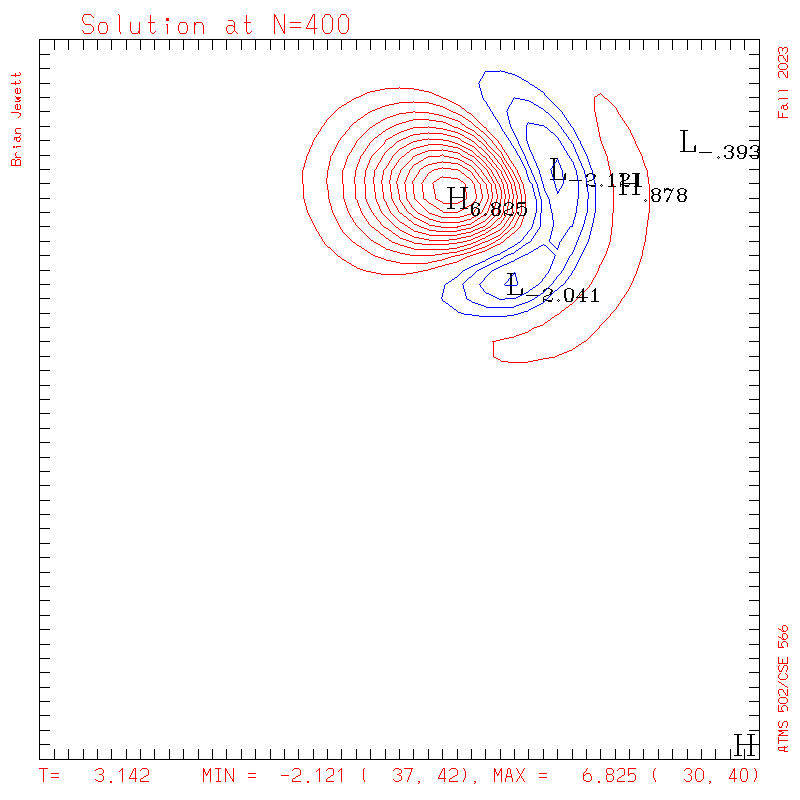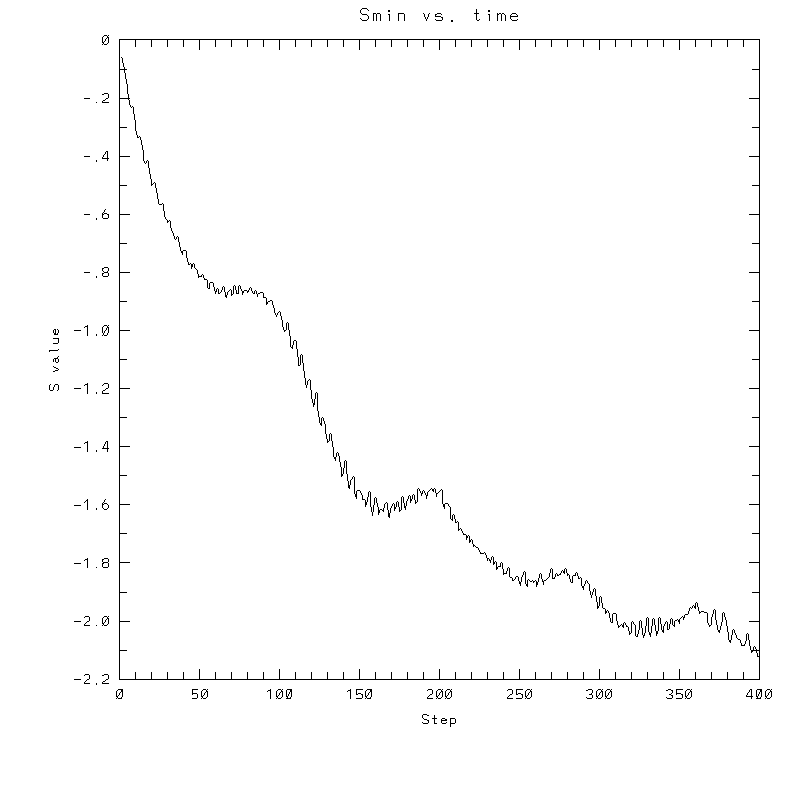Lax-W surface 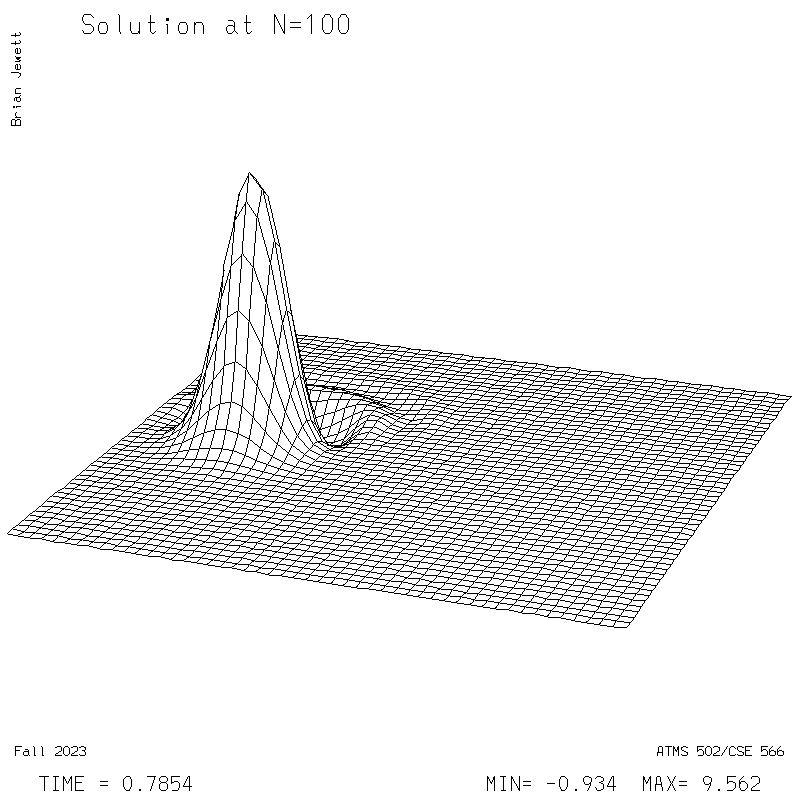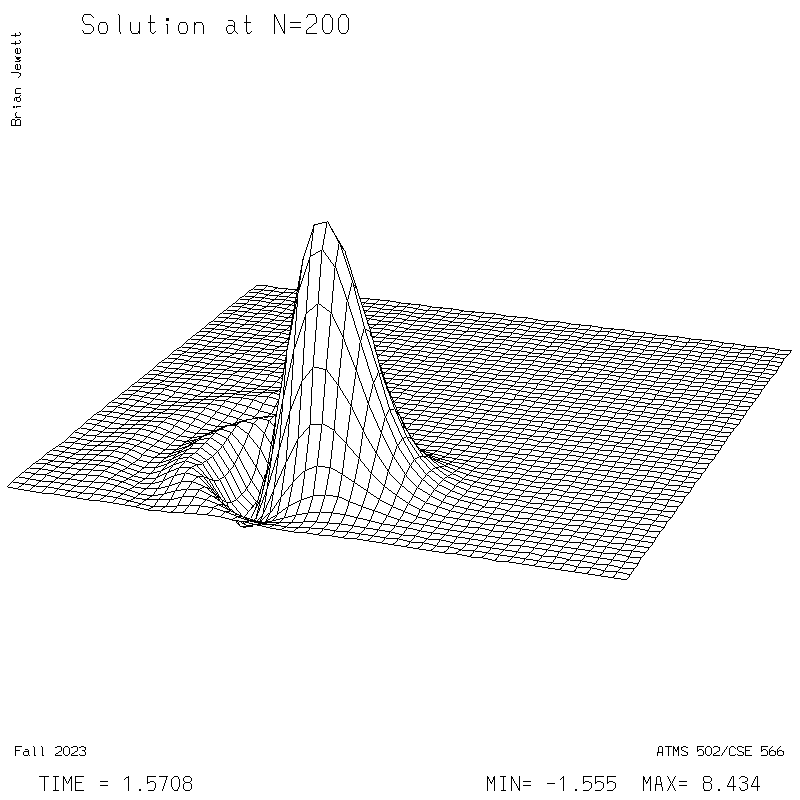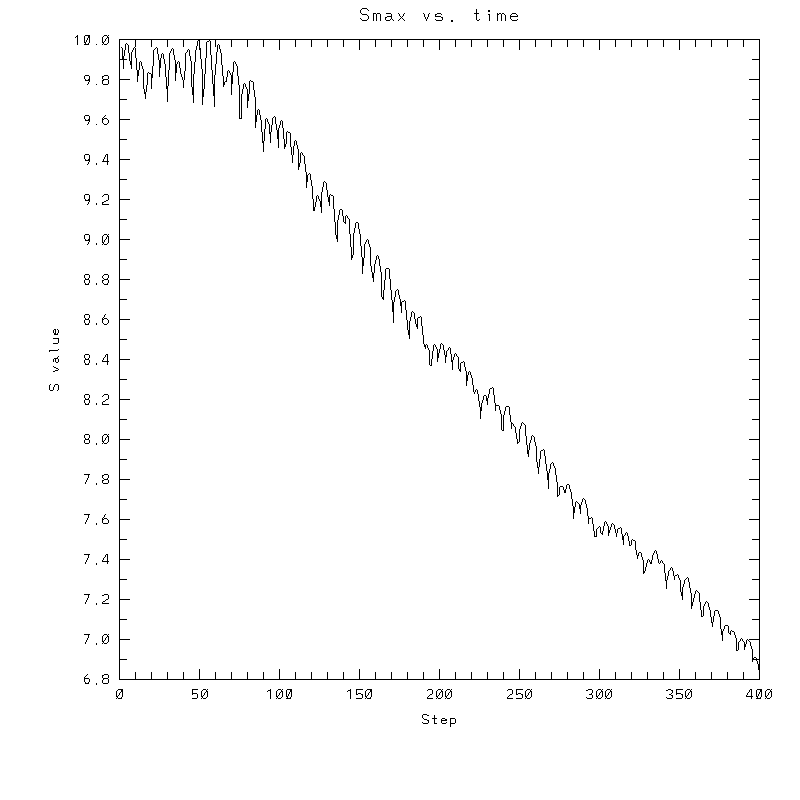Takacs contours 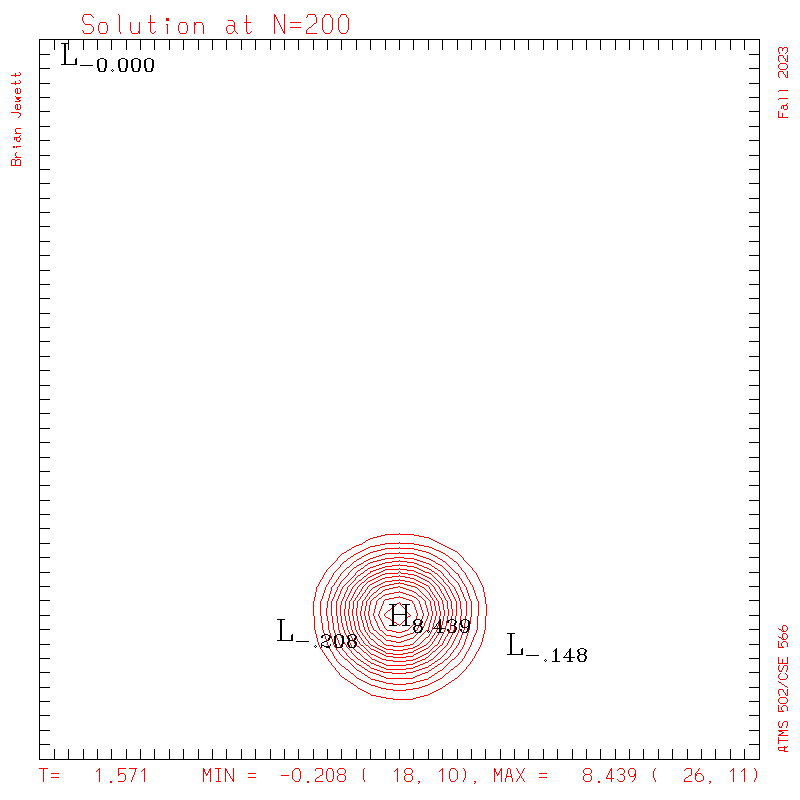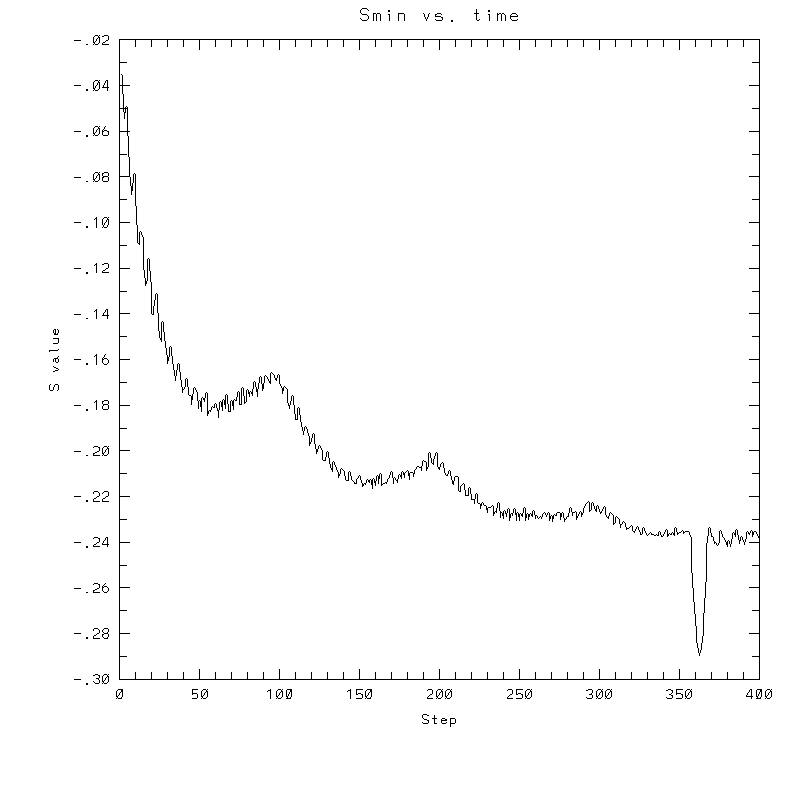Takacs surface 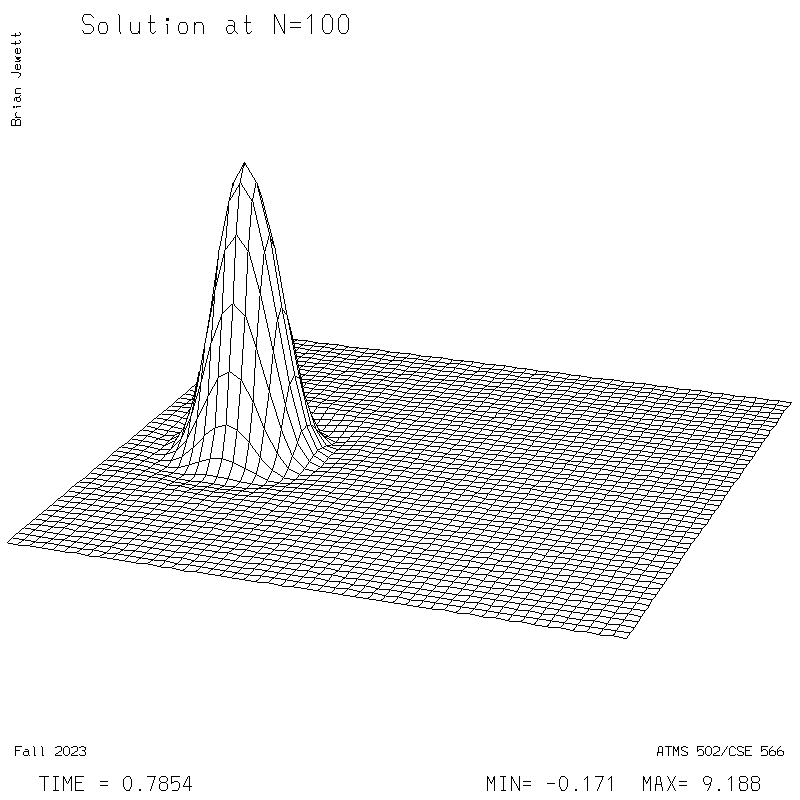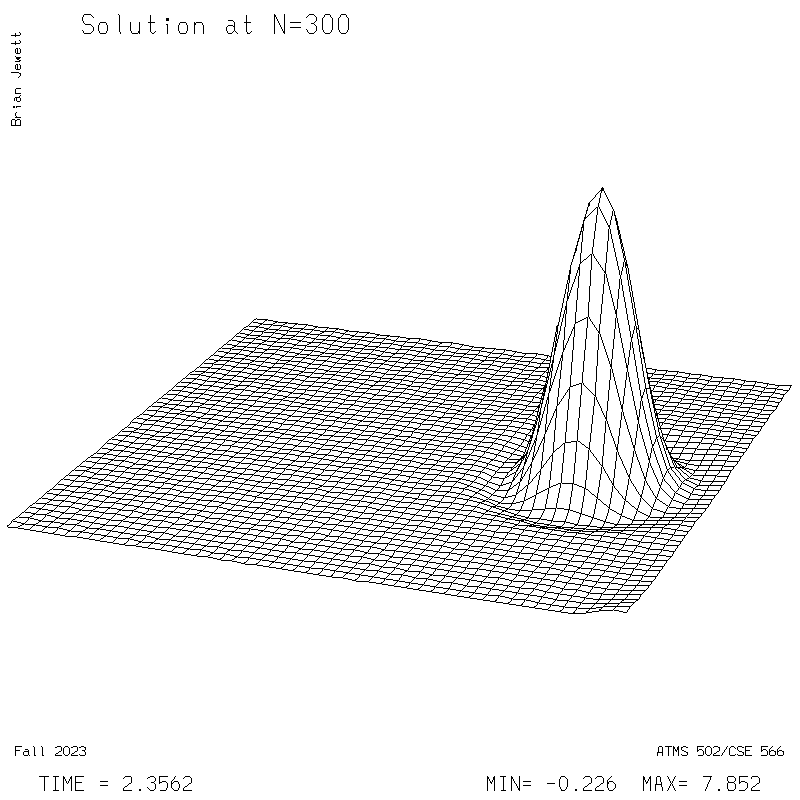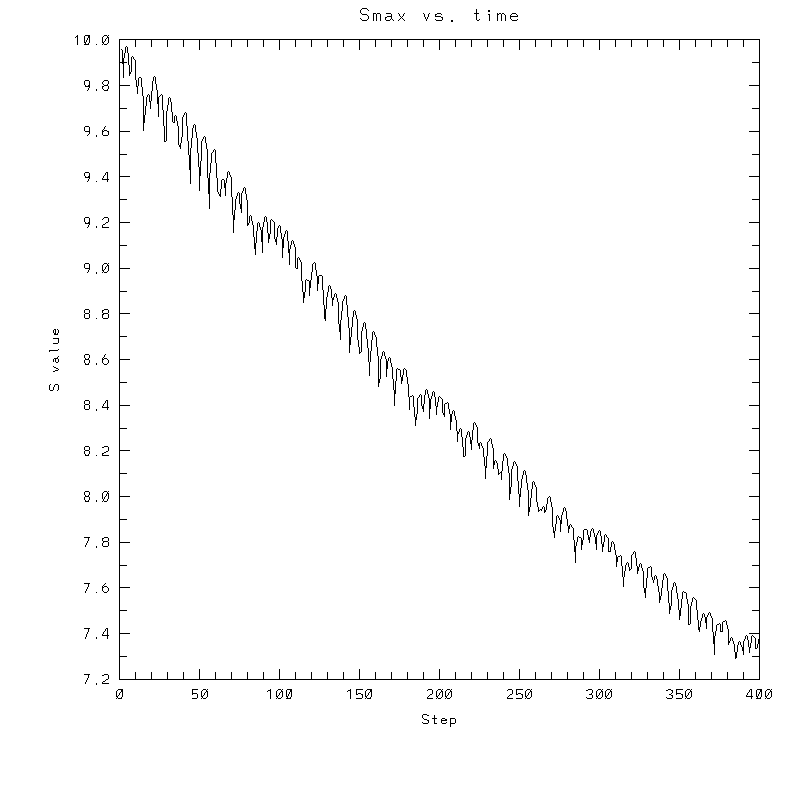Crowley 6th contours 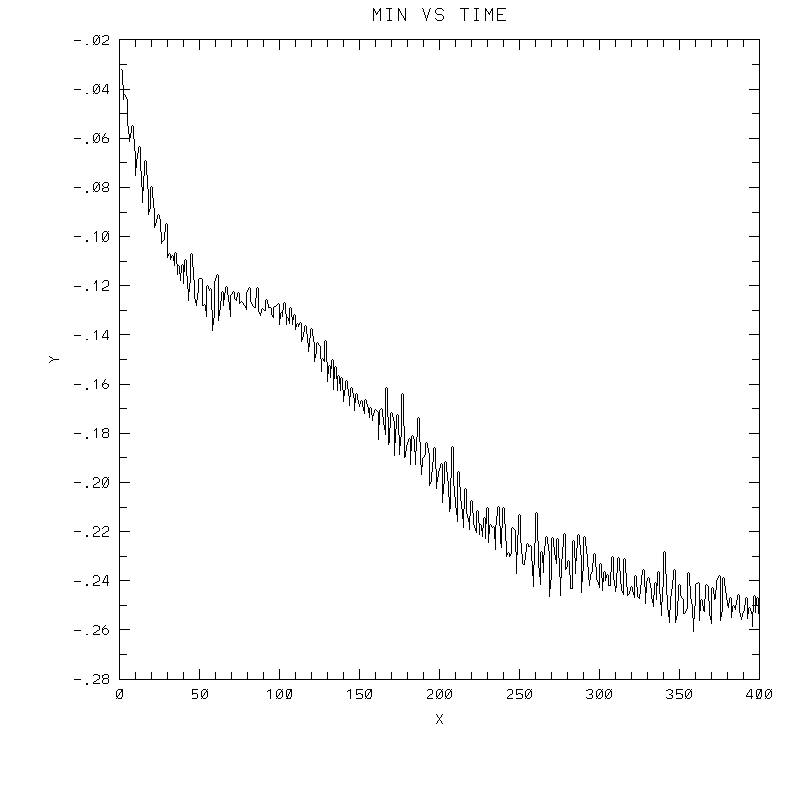Crowley 6th surface

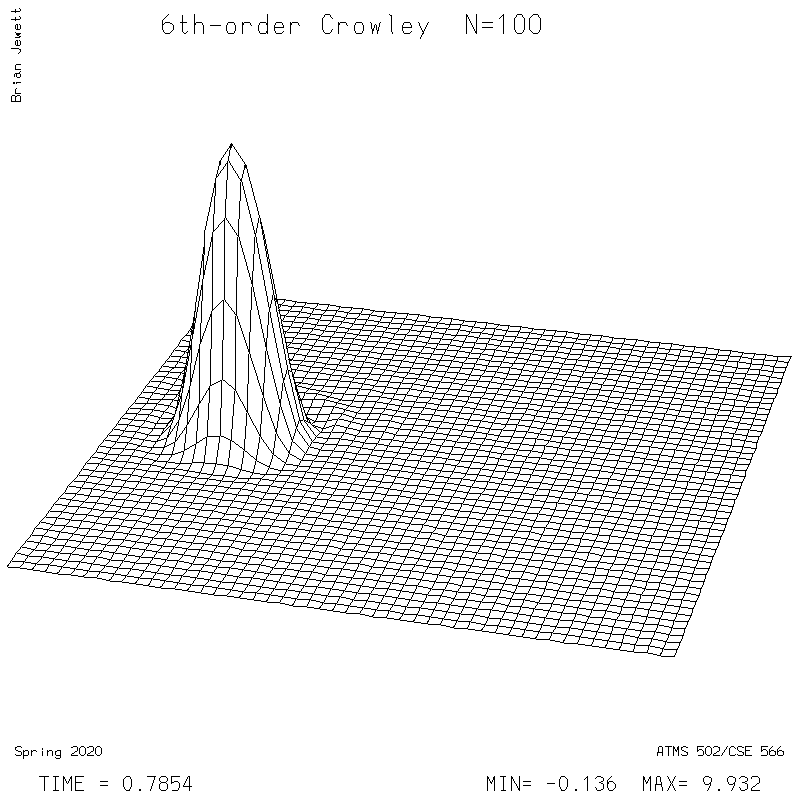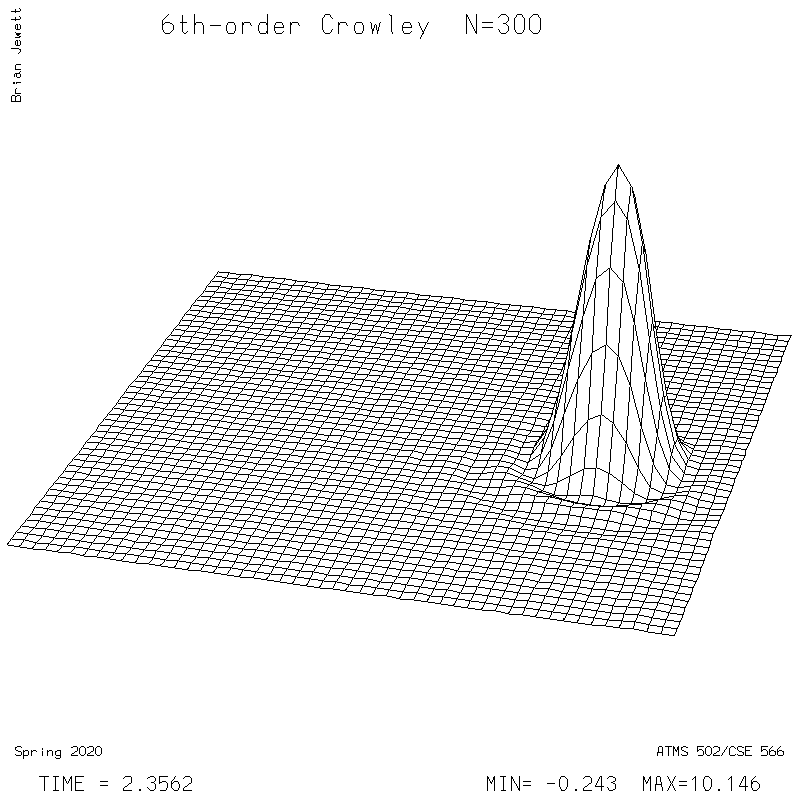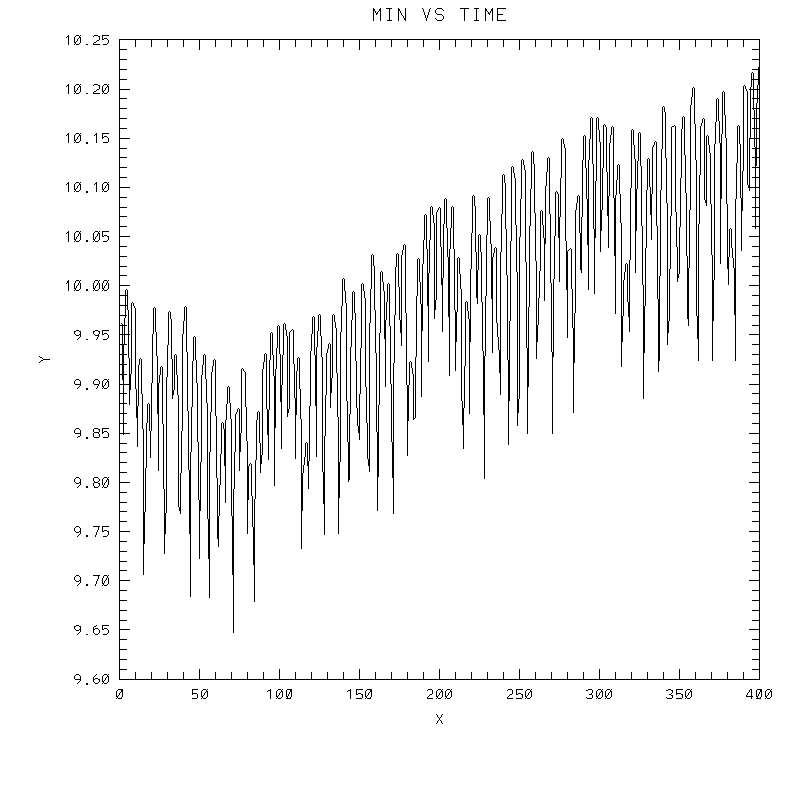Frequently asked - and new - Questions & Answers - most recent first. 

1. [Getting Segmentation Fault]
   
   
   Particularly if this happens when plotting, make the character string "title" -- which is passed to
   routines contr and sfc, larger than the default size of 25 letters long (e.g. try 50 instead).
   
   
2. [Getting skewed, very un-cone-like initial condition plots]
   
             You likely are passing an array with ghost points to the plot routine -
              and our plot routines are not expecting an array with ghost points.  To fix:
   
            • In C, copy your s1[][] or s2 array to a separate array of [NX][NY] size and call contr or sfc with that, e.g.
   
                float splot[NX][NY];
                for ( j=J1; j<=J2; j++ ) {
                  for ( i=I1; i<=I2; i++) {
                    splot[i-I1][j-J1] = s2[i][j];
                  }
                }
                contr( NX, NY, splot, ... )   (same sort of thing is done for calling sfc)
   
            • In Fortran, be sure and pass the "real" (no ghost zones) part of your array, i.e. use array subdomains as shown below:
   
                call contr( nx,ny, s2(1:nx,1:ny), ... )
   
   
3. [Concerns over U and V flow array sizes]
   
             Our U array is (nx+1,ny) and V is (nx,ny+1).
             When doing X-advection, we need to pass the nx+1 values in the first dimension of U.
             When doing Y-advection, we need to pass the ny+1 values in the second dimension of V.
             C programmers: Note also that in advection, you use the i1, i2, j1, j2 when copying s1 or s2; but u and v have no ghost points.
                 ... so you have to be careful with indices. 
   
   
4. My min/max values and plot vs. time for the official problem is very different from the 51x51 test case ...
   
             Yes, there is much more resolution and the waves are much reduced and smax(t) looks very different.


5. I encountered problems when updating my history(nx,ny,step-counter) array
   
           There is no need for a history() array in program 2. 
           So please delete the history() array definition, and the loop(s) used to create it.
   
   
6. Do the 121x121 dimensions include ghost points? 
   
            No - the ghost points are in addition to the physical 121x121 (or 51x51 for testing) grid sizes.
            And, only the scalar S array is 121x121; U and V dimensions differ due to the staggering.
   
   
7. Why do my contour plots have fewer contours than yours?
   
            Check to make sure you are using the same contour interval when plotting, if you want to match my results.
            I used a contour interval of 0.5 for s1 and s2, and 0.1 for u and v.
         
   
8. Do I need to pass 'ghost points' for the scalar "s" arrays to my advect1d routine?
   
            Yes.  Make sure your 1-D array for s1 is dimensioned to include ghost points, and have your advection routine
            copy all of a row or column - including ghost points - to the 1d array that you pass to advect1d.
   
            Advect1d only changes the 1:nx (in Fortran notation) grid points, but it uses 0:nx+1 (again considering the Fortran case).
   
   
9. What grid dimensions do I need - are there ghost points for all arrays?
   
   
   You only need ghost points for the "s" arrays, s1, s2, and strue. 
   The X-velocity is dimensioned u(nx+1,ny), and the Y-velocity is v(nx,ny+1).
   
   
   
10. How we should use the advect1d subroutine each time?
    
    
    All the advect1d routine "knows" is that it is getting a 1-D array of a field "S", and a velocity field - say, call it "vel1d" (we used to just consider this a constant "c").  It takes the N-time level values and returns the N+1 time level (updated) values.  It doesn't actually care whether it is being used in X- or Y-advection.
    
    
    
11. There are two common formulas for variance. One is: Sum[(X-mean(X))^2] over all X, and divided by N, the total number of points. The other possibility is dividing by (N-1) instead of N. I just need to make sure which to use.
    
    
    I am using the (sample, biased) variance expression:
    
       variance = 1/N * sum[ (s(i)-smean)**2 ]
    
    For more on the difference between these two types of variance, see this page at MathWorld.
    
    
    
12. When should I use the subroutine plot1d? is it used to draw the smax, smin versus the time step?
    Do I need to change plot1d to 2-D?
    
    
    There is no need for plot1d, though you may use it if you wish as we did in program 1. 
    A simpler approach:  To plot a 1-d array such as the minimum S values vs. time step (what I call smin), do this:
    
        call ezy(smin,nstep,'Min value of S vs. time')
    
    In C,
    
        c_ezy( smin, nstep, title );   (smin is float *, nstep is int, title is char *)
    
    For more on the ezy routine, see this online documentation.
    
    
13. My contour plots look the same, with the same smax and smin values as your examples, our final error values are slightly different.
    
    
    It is probably a matter of coding the calculations slightly differently.  As long as they are somewhat close to mine and your contour plots look the same and your dissipation + dispersion error adds up to your total error, don't worry about it.
    
    
    
14. [Plotting S array when calling contr routine in C]
    
    
    You may recall that the plot routines we are using expect arrays dimensioned NX (in program 1), and NX,NY in this program.  Thus, I recommend copying your s2 values (s2 being dimensioned NXDIM,NYDIM) to a new NX,NY array - so the array passed to contr() is of size [NX][NY] and the values start at array location [0][0], not [I1][I1].  Here is one way, for the initial condition:
    
              float plot_s[NX][NY],runtime;
          ...
              sprintf(title,"Contour plot at n = %d",n);
              for (j=I1; j<=I2; j++) {
                for (i=I1; i<=I2; i++) {
                  plot_s[i-I1][j-I1] = s2[i][j];
                }
              }
              contr(NX,NY,plot_s,cint,0.0,title,colors,pltzero);
    
    In Fortran, there is a shortcut for this: call contr(nx,ny,s2(1:nx,1:ny),...) but in C we need to specifically pass an array of NX,NY size.
    
    C programmers: Note the 'time' expected as an argument to contr() should be float, not integer - pass "0.0", not 0, and use a float variable or calculation during the run, e.g. contr(...,dt*(float)n,...) or something along those lines.
    
    
    
15. [Plotting smin and smax time series array at the end of your program]
    
    
    In this 2d program you are asked to plot both the min and max values over time, rather than just the max absolute value.
    I suggest getting rid of strace() and defining new arrays, smin() and smax(), of size MAXSTEP - make sure maxstep is at least 600.
    Then, in your main program, in your big n=1,nstep time integration loop, call your stats routine passing it the location of the one element of the smin() and smax() arrays that you want to set for the current time step.  In FORTRAN,
    
          call stats(s2, ..., smin(n),smax(n))         in FORTRAN                                                                  --  so smin(1) is first value stored.
          stats(s2, ..., &smin[n],&smax[n]))        in C -- if your time step loop runs (n=0;  n< nstep;  n++)  -- so smin[0] is first value stored.
          stats(s2, ..., &smin[n-1],&smax[n-1]))  in C -- if your time step loop runs  (n=1; n<=nstep; n++) -- so smin[0] is first value stored.
    
    Then, after your main time step loop has finished, you calculate your Takacs-style error statistics, and also plot your smin and smax arrays using the ezy (or, in C, c_ezy) routines - one call for smin, and the other for smax - to plot nsteps time steps.


16. [Not evolving correctly or S field is not changing at all with time]
    
    
    I suggest this.
    Comment out all Y advection steps.  Use only X advection.
    Set the U array to be 1.0 everywhere (in the real problem, U ranges from -1 to +1).  Set V to zero.
    Now run your code for 20 steps, plotting every step.  The cone should move to the right.
    Put print statements in the integration and advect routines to find out what is happening if it does not move correctly.
    
    Then put Y advection back and comment out X advection.
    Set U to be zero everywhere.  Set V to be -1.0 everywhere.
    Run the code; the cone should move down towards lower Y, towards the center.
    Again, if it isn't working, I would do debugging from the inside out; run one time step, print out results inside advect1d, and make sure values are being updated and the one-dimensional S, U (or V) and dt and dx values are OK.  When that is working, go to your integration step (where advect is called) and make sure you are updating the 2-d s1 or s2 arrays correctly with the output from advect1d, and that you are not somehow overwriting your new (updated) values by doing an incorrect update within the integration step.